Kyle Wang

Current M.S Robotics Student

Table of Contents

  • Video Demo
  • Overview
  • Conclusions

    • This was the final project of Northwestern University’s ME314 Machine Dynamics class, and focused on Lagrangian dynamics in rigid body systems. This project analyzes Lagrangian dynamics including external forces, constraints, and impacts, and was developed using the Sympy, Numpy, and Plotly packages in Python. I chose to model a dice bouncing around in a box. Both objects experience external forces (gravity), impacts, contstraints.

    Source code: Google Collab

    Video Demo

    Overview

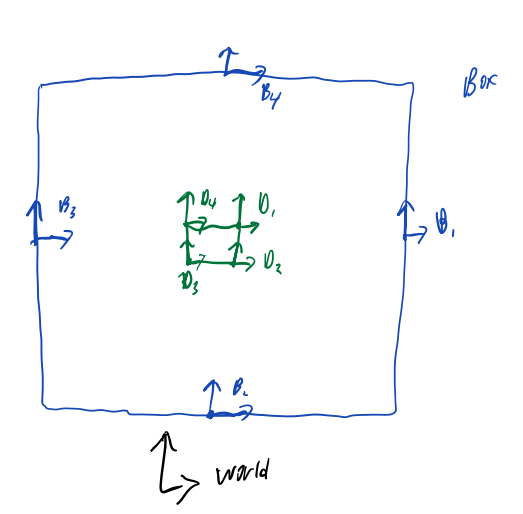
    I started by defining the transformations needed:

    • The world frame to the box and dice frames
    • The walls of the box to the center of the box
    • The walls of the dice to the dice

    In order to calculate the Lagrangian, I calculated the potential energies of the box and dice (using the masses and the y values) and the kinetic energies (using the Twists and Inertia Matrices). Using the Lagrangian, I calculated the Euler Lagrange equations.

    I constructed the constraints using the transforms from the box walls to the dice vertices. To ensure that the dice stays inside the box, I checked if any vertex of the dice is in contact with, or extremely close to, the wall.

    For the external forces, I chose an upwards force equal to the gravitational force on the box - this way, the box position would remain constant. I also gave the box an initial angular force so that the collisions and rotations were easier to see - the animation wouldn’t just show the dice bouncing up and down. Because of the initial angular velocity and the collisions, the resulting animation shows the box spinning in one direction, stopping, then spinning in the opposite direction. I played around with the numbers for the external forces so that the angular force changes over time and the trajectories vary

    Frames

    Conclusions

    The simulation works as expected. The dice bounces around in the cup, and experiences collisions that result in it spinning around. There is a large difference in mass between the dice and the box, which is clear since the dice bouncing around does not affect the rotation of the box by much. It also doesn’t affect the box’s x or y positions